July 18, 2021 by ゴールド

数弱必見！！浪人で数学を伸ばした男の勉強法！

自己紹介

こんにちは！東大理一２年のゴールドです。
　

僕は関西の、東大は大体年に一人ぐらいの高校出身です。東大を目指す人で、僕と同じような境遇の人も多いのではないでしょうか。
　

高３の５月まで部活をばりばり続け、本格的な受験勉強は高３から始めました。
文武両道で現役合格！……が理想だったんですが、あと少しの所で落ちて、悔しい思いをしました。
　

そして某S台予備学校で一浪した後、合格を果たしました。その際伸びにくいと言われる数学を数弱ながら15点以上伸ばして合格したので、その際の勉強法をお伝えしたいと思います！
浪人生はもちろん、高校生にとっても役に立つと思いますので、ぜひ読んでください！
　

はじめに

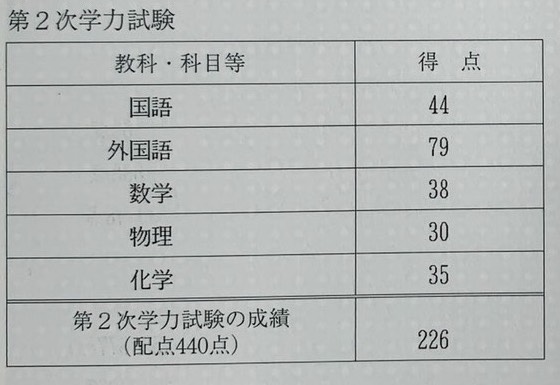
はじめに、僕の現役時代と浪人時代の得点を載せておきます。
　

現役時

　

浪人時

　

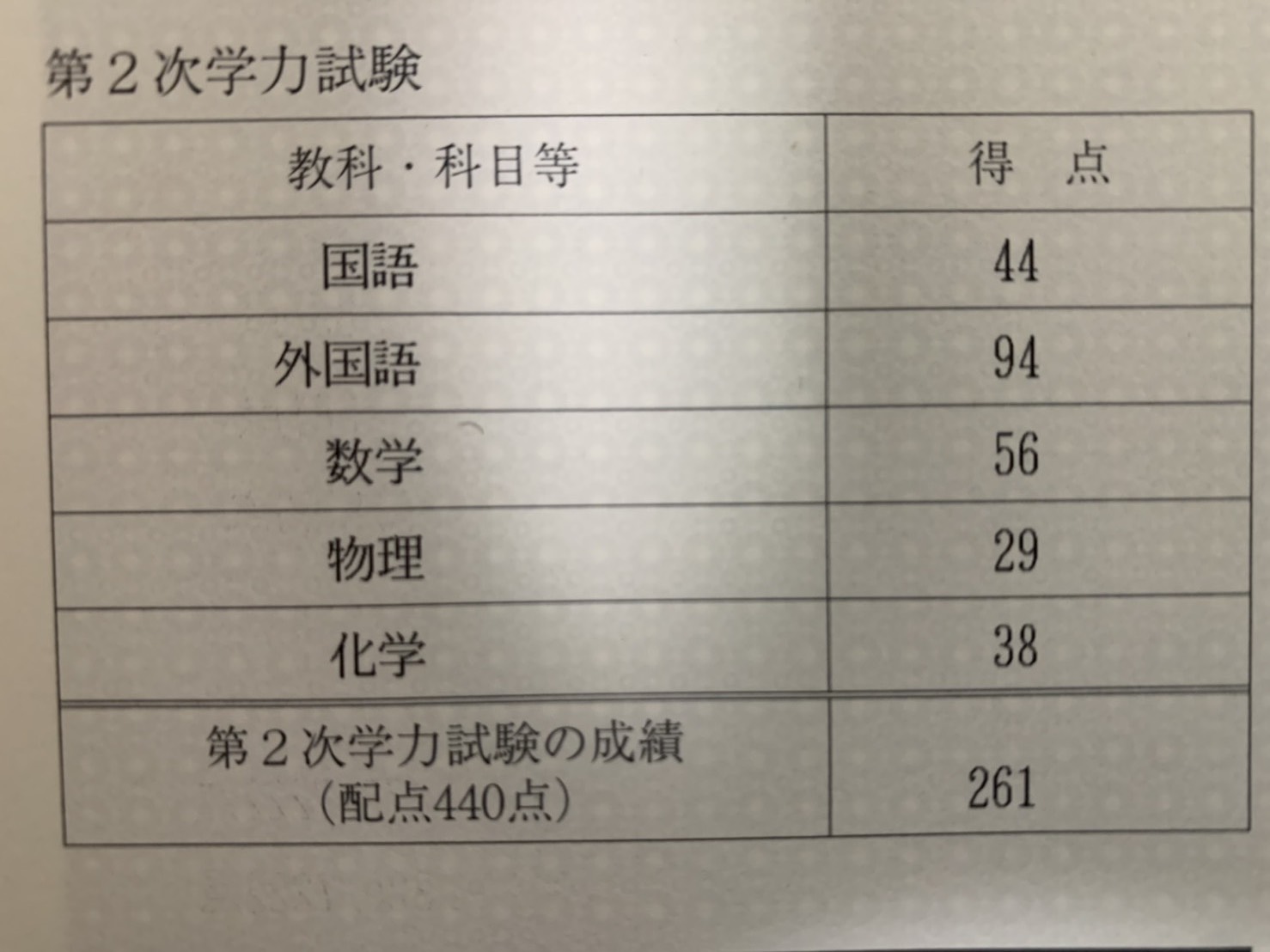
数学は低いですね。英語は高いですね。しかしどちらも15点くらい伸びています。理科はほとんど変わっていませんね。（浪人中なにしててん）
　

まあ入試の採点というのは、その時の生徒の出来によって調整されるものですから、この数字通りの出来というわけでもありませんが。（現役時の物理なんか絶対半分もできてへんし。）
　

ただし、数学と英語に関しては浪人の年には「難化した」と言われていたし、合格点も下がっているので、実力が伸びたことは確かだろうと思っています。
　

あと、数学は浪人時でさえ56点なので、数弱です。数強（の一部）のように、「数学？感覚でやったら解けるわw」とか言いません。安心してください。
　

また、数学が苦手な人、特にセンターとか地方国公立レベルの問題なら解けるけど、難関大の数学となると全然ダメ…… という人は特に参考になると思います。
僕のかつてやっていた悪い勉強法になってしまっている可能性が高いと思うからです。
　

数学で大切なこと

僕が思うに、数学は論理的に考えて解法の本質をつかむことが何よりも大切です。具体的には、公式の証明や、解答の立式の理由（どうしてそれが嬉しいのか）を明確にすることが重要で、解法をひたすらに暗記するような癖はなくすべきです。
　

例えば確率の問題を解く時、みなさんはどうしているでしょうか。
「確率か、どうせ漸化式やろ。とりあえずPnとPn+1の関係調べよー。」
という感じで、何も考えず、過去に解いた確率漸化式の問題の解き方をそのまま当てはめようとする人もいるかもしれません。
　

しかし！確率の問題だからといって漸化式を使うとは限りません。また仮に漸化式を使うとしても、二項間漸化式とは限りませんし、Pnのnは何をnにとるのがよいのかも考えるべき（偶奇の場合分けなど）です。ただ知っている問題を思い出してその解き方をあてはめているだけでは、解いたことのある問題しか解けません。

当然ですが、東大入試の問題は全問初見の問題が出ます。東大数学の過去問を解いたことがある人なら分かると思いますが、典型問題やその類題が出ることもほとんどありません。ですから、初見の問題を解けるようになる練習をすべきです。
　

初見の問題を解くためには？

ではどうすれば初見の問題が解けるようになるのでしょうか。
　

世界で初めて確率漸化式を使った人は、このように考えたはずです。
　

うーんこの操作、何回も繰り返すんか。とりあえず1回ずつやってみよ。
えっと、1回目の操作(n=1)は、こうなるんか。2回目の操作はこうか。なるほど。じゃ3回目は……
ん、まてよ！これって常にn回目とn+1回目の確率、互いに関係してるやん！しかもn回目にA（という事象）になる確率をPnとすれば、PnでPn+1を表せるやん！！　ほんならこれ、数列でやった漸化式になってるやーん！よし、これなら解けるぞ！！
　

そう、本来は問題を読んだだけでは漸化式とか思いつくはずがないのです。上で書いたように
　

実験した上で（PnでPn+1を表せるのを把握した上で）、今まで経験した解法の考え方（数列の漸化式という考え方）を借りて
　

解法を思いつくものなのです。
　

今まで経験した問題の解法がそっくりそのまま使えることは少ないです。
　

むしろ、解法の考え方のうち、使えるポイントだけ借りて自分で答えまで辿り着くものなのです。（今回なら、「n+1回目の値を1〜n回目の値で表せる場合は、漸化式を立てることでn回目の値が求まる」というポイント）
　

このように、問題を読んでから解法を思いつくプロセスこそ、最終的には入試に向けて鍛えるべき所なのです。
　

数学の勉強法

数学力には次の二つのベクトルがあると思います。

A:各解法を正確に運用する力

このBができていない人が多い気がします。解答を読んだだけで満足せず、自分でその解法を思いつけるようになることを目指しましょう。
　

また、Aは解答を読めばわかりますが、Bは分からないことも多いと思います。そんな時は信頼できる先生や友達に質問しましょう。
聞ける相手がいなければ、東大Passportの相談会にお越しください！！！
　

問題を見たときに解法を思いつくプロセスを鍛えたいので、数学の勉強をするときは、まずは自分で解法を考えてみましょう。
解けなければ答えを見ても構いませんが、必ず
「その解き方をどうやったら思いつけるのか」
を考えましょう。これを突き詰めることが本当に重要です。
　

数学の解法をひらめくためのコツ

最後に、頑張って考えても問題が解けるようにならない！という方向けに、僕が受験勉強をしていて思いついた、適切な解法をひらめくためのコツをいくつか紹介しておきます。
　

①単純な状況で実験してみる

上の漸化式のときのような考え方です。
整数のnとかが出てくれば、まず1,2とかを入れてみる。
よくわからないf(x)が出てくれば、xに簡単な数字を入れてみる。
そこから何か一般的な法則をつかむ。これは整数や確率の問題に特に有効です。
　

②問題の情報を俯瞰する

当然ですが、解答は、問題文の情報から導けるように出来ています。問題が解けないのは、情報を見落としているか、情報の使い方、組み合わせ方が間違っているからです。問題文を読みながら情報をまとめ、全体を俯瞰して考えます。
　
僕は下の画像のように情報に下線を引きながらまとめていました。
問題文を読んだだけでは、nとかkとかｍとかややこしいので、それぞれが何を意味しているか一目でわかるように線を引き、整理して、問題の情報全体を一度に把握できるようにしていました。
右上の方のa3,2というのは、①の方法の、実験の痕跡です。

2020年度東京大学入学試験問題　数学（理系）第４問　（実際に僕が入試本番で使った問題用紙です！）
　

③とばす

いやそうはいっても、考えたけど分かんないよ……となったら、これです。
　

皆さんテスト中に解けなかった問題について、テスト終了後にちょっと考えた途端解き方を思いつく、なんて経験はないでしょうか。よくありますよね。（僕はありました）
一旦気分転換して、時間をおいてもう一度考えると、どうしてか急に解けるようになる時があります。（多分無意識のうちに頭のどこかで考えているのだと思います）
　

一旦気分転換に別の問題を解き、また戻ってくるのです。
本番でも、分からない問題があれば、時間も限られているので、飛ばすことは重要です。
　

このような姿勢で数学に取り組めば、初見の問題を解く能力が鍛えられ、これまで暗記解法に頼っていた人は特に、難関大学の数学の成績が大きく伸びると思います。
　

最後に

受験は苦しいこともあるかもしれないですが、合格すれば夢のオンラインキャンパスライフが待っています。頑張ってください！！
　

これからも東大Passportは様々な活動を企画しているので、ぜひ以下のSNSをチェック！！

Twitter(@todai_passport)

Facebook

公式ライン